Why is Life so Difficult? – Unveiling The Magic of Complex Systems Science

Life has an uncanny ability to present us with challenges and difficulties that often leave us wondering why it has to be so hard. The complexities of our existence are intertwined with a myriad of factors, making it a fascinating and perplexing journey.

In my main article on ‘Why Life is So Hard?’ – we had covered how formation of Power Laws in life leads to making life difficult. We had specifically seen that “Randomness Over Time” leads to Power Law formation where the top 20 percent get 80 percent of wealth.

The next natural question on my enquiry into the question “Why life is so Hard?” was – “What causes Randomness in Life?””

Finding the answers to these questions led me to a new branch of science called as Complexity Science.

Complexity Science is a powerful lens through which we can understand the intricate nature of life.

Complexity in nature introduces randomness in life and ends up causing is myriad difficulties.

My journey into Complexity Science begins with the understanding of the magically named Butterfly Effect and Chaos Theory.

In this article, we will explore why life is so difficult by delving into the fascinating interplay between Complexity, Chaos and Order.

What is Complexity Science?

We live in an era of Science and Technology. Science is amazing and it has given us amazing tools.

Unfortunately, the way Science is taught in our school, Science seduces us to believe that there is a straight-forward solution to every problem. The problem is that majority of our textbook Science deals with ‘Simple Science’.

‘Simple Science’ deals with simple cause and effect. If you do ‘A’ then it will lead to ‘B’. In simple science, no randomness is involved. Simple science models always produce the same output from a given starting condition or initial state.

Unfortunately, randomness is part and parcel of the very fabric of life. Simple formulas don’t exist.

This presence of randomness leads us to the science of Complexity.

The most surprising thing about Complexity Science is that it produces different outputs even if given the same starting inputs!! And it is not absurd.

The reason for this is what lies under the hood of Complexity Science.

Under the hood of complexity science lies multiple formulas which effect each other.

A impacts B and C, C impacts D and B, B impacts E and F, F impacts E and A.

When the formula inputs start impacting each other, it leads to things like Feedback Loops and iterative calculations.

This interconnection between inputs leads to Complexity Science where same starting inputs can lead to different outputs.

With our current scientific education based on Simple Science, our core belief becomes that everything around us is Simple with simple cause and effect. Most of us believe that each observed effect has a clear cause linked to it.

Due to this education, most of our Belief Systems are being prepared in a way which teaches us that the Human Race has solved it all. If something is problematic, then it is the fault of the individual, who is being unscientific or who is lazy.

We have mapped the whole world. We know the complete weather system of the world. With our mobile phones, the whole world is in our pocket. We can book tickets to anywhere, reach there, experience a new world and come back. Everything works.

Till it doesn’t!!

Like the Covid19 Pandemic!

When everything got shut down!

You see, impacted by inter-connectedness, everything has an element of randomness to it. All worldly natural systems, including human beings are Complex systems.

These natural systems are like weather systems. You know that it’s the hurricane season – but you are never sure if a Category 5 hurricane will hit a particular place or not. It could and again it might not.

It is like the World Cup Football Final. Argentina won, but so could have France.

It is like our money systems.

We put our hard-earned money in a company – but again we are never ever sure if that company will take off and give us an attractive return or whether that company will turn out to be a bust like Enron or Theranos (a health-tech company which turned out to be a scam).

It’s like the Tsunami of 2004 which caused a million deaths in the Indian Ocean. Or like the Earthquakes which keep on shaking parts of world – sometimes minor shocks and at other times devastating. This is Real Life Science, now called as Complexity Science.

Living in this complex world, we all take risks and pray that things may turn out to be ok.

Our world is so large and mystical, beautiful yet scary, known yet unknown, connected yet distant. This is the world’s magical nature of being an ever evolving, non-deterministic and complex system.

If you have followed my journey, I was so frustrated at not losing weight that when I did in only two months – I started calling the whole process as Magical.

As I studied complex systems, I realised that they are actually the Magic in our lives. The magic which is everywhere. The magic which is in our environment making us act on its own volition.

Now, let’s understand these complex systems by looking at the aptly named phenomenon called as the Butterfly effect.

The Butterfly Effect – The Foundation of Chaos Theory

The Butterfly Effect is a concept derived from Chaos Theory. The fundamental premise of the Chaos theory is that a small change in one part of a complex system can lead to significant effects in another part of the system.

Edward Lorenz, a weather scientist, coined the term Butterfly Effect, when he made an accidental discovery that shattered his expectations and forever transformed our understanding of the natural world.

The name ‘Butterfly Effect’ symbolizes Lorenz’s discovery that the mere flap of a butterfly’s wings in Brazil can cause a hurricane in Texas. Let’s see how!!

Edward Lorenz used to imagine a ‘Simple Science’ world where the future could be accurately predicted with precise calculations and equations. A world where the mysteries of nature could be unfolded before our eyes, guided by simple equations that govern everything around us.

Lorenz formulated an intricate system comprising twelve interdependent equations to decipher the intricate patterns of weather phenomena.

In this intricately interconnected web of equations, each weather parameter exerted influence upon others. Factors such as pressure affecting winds, winds impacting temperature, and temperature in turn influencing pressure.

To obtain accurate predictions, Lorenz had to iterate these equations numerous times, a computational challenge that necessitated the use of early computer technology available during the 1960s.

One seemingly ordinary day, Lorenz was running a numerical computer model to redo one of the earlier weather predictions.

To save time Lorenz opted for a shortcut.

He inputted values from a printout that corresponded to a specific moment in the midst of the prior calculation.

Allowing the computer to proceed with its task, Lorenz leisurely strolled down the hallway in search of a revitalizing cup of coffee, oblivious to the extraordinary events about to transpire.

Upon his return, a mere thirty minutes later, Lorenz was met with a confounding revelation that defied his expectations.

In those thirty minutes, the computer had regenerated two months of predictions.

But instead of reproducing an identical outcome, the computer had generated an entirely new and divergent result.

Initially suspecting a malfunction in the computer’s vacuum tube, Lorenz hesitated to call upon technical assistance.

Instead, he meticulously re-evaluated the data, and in this process, a glimmer of insight illuminated his path.

Lorenz noticed that the initial values generated by the computer nearly matched with the earlier output. There was only a minor difference.

Tracing the minor difference, Lorenz realised that he had entered the value of 0.506 from the printout rather the full precision value of 0.506127 which was the value in the earlier computer iteration. He had omitted 0.000127.

This seemingly minor difference of 0.000127 kept on doubling every four days till the predictions completely changed in the middle of the second month. Instead of calm weather, a raging tornado was now predicted!!

This extraordinary revelation, aptly termed the Butterfly Effect, unveiled the hidden intricacies of complex systems.

It illuminated the profound truth that even the slightest alteration in initial conditions—the gentle flutter of a butterfly’s wings in a distant land—could set forth a chain of events that reverberates across space and time. Ultimately leading to dramatic and unpredictable consequences, such as the birth of a hurricane thousands of miles away.

Lorenz’s ground-breaking paper on Chaos Theory reverberated throughout the scientific community, engendering a paradigm shift in our understanding of predictability within complex systems.

It shattered the long-held assumption that accurate long-term forecasts were attainable and instead opened a Pandora’s box of profound inquiries about the inherent nature of our universe.

The Butterfly Effect emerged as a powerful symbol, underscoring the intricate interconnectedness of our world and emphasizing the potential ramifications embedded within seemingly inconsequential actions.

Logistics Maps and the birth of Chaos Theory

The next big insight in Chaos theory came from a biologist Robert May and his mathematician friend James Yorke. Robert May was using a form of equations called as Logistic Maps to model animal population growth from one year to the next.

The idea behind these equations is that the next year’s population would be a function of the current year’s population and the resources required to sustain the population.

Hence, if the population of current year is more, the reproduction will be more. But if the population is too large, then the resources to sustain that population will be constrained. This lack of resources for a larger population will reduce population growth.

The Logistic Maps equation takes the form of:

x_n+1 = γx_n(1-x_n),

• where, n is the current year, n+1 is the next year and lambda(γ) is a constant and acts as a proxy for environmental conditions.
• x_n implies proportionality to population size (more population leads to more growth).
• (1-x_n) reflects the resource constraint (more population leads to lesser resources).

The logistic map is plotted when you plot x for different values of lambda.

While plotting the Logistic Map, Robert May observed a very curious behaviour in these logistic maps.

Till lambda is below 1, the population x always goes down to zero. Hence, a lambda below one indicates that environmental conditions are not conducive for that particular animal.

Beyond a lambda of one, the population x initially keeps on rising.

But once lambda passes three, the value of x starts fluctuating between two stable values. One year the population is higher, then the next year it is lower and so on. Hence, the population repeats in the same pattern for every two years.

On increasing lambda further, the population x starts to fluctuate between four values.  Hence, the population pattern now repeats every four years.

On increasing lambda further, this repetition period becomes eight as the population x oscillates regularly between eight values.

This predictable doubling of repetition as lambda is increased has a technical name and is called as ‘Period Doubling Bifurcations.’

However, as lambda surpasses 3.57 a very interesting thing happens. This predictable Period Doubling Pattern abruptly disintegrates plunging the population x into a realm of completely random and chaotic fluctuations.

However, the mind-bending nature of Logistic Maps does not end there.

By continuing to increase lambda, the chaotic fluctuations of x yield to order once again!!

And more surprisingly, as lambda increased further, Chaos resurfaced, setting forth a perpetual dance between Order and Chaos.

The cycle repeated itself: Order, Chaos, Order, Chaos. This is what the whole diagram looks like. The dark areas are the Chaos and the white are the ones with order.

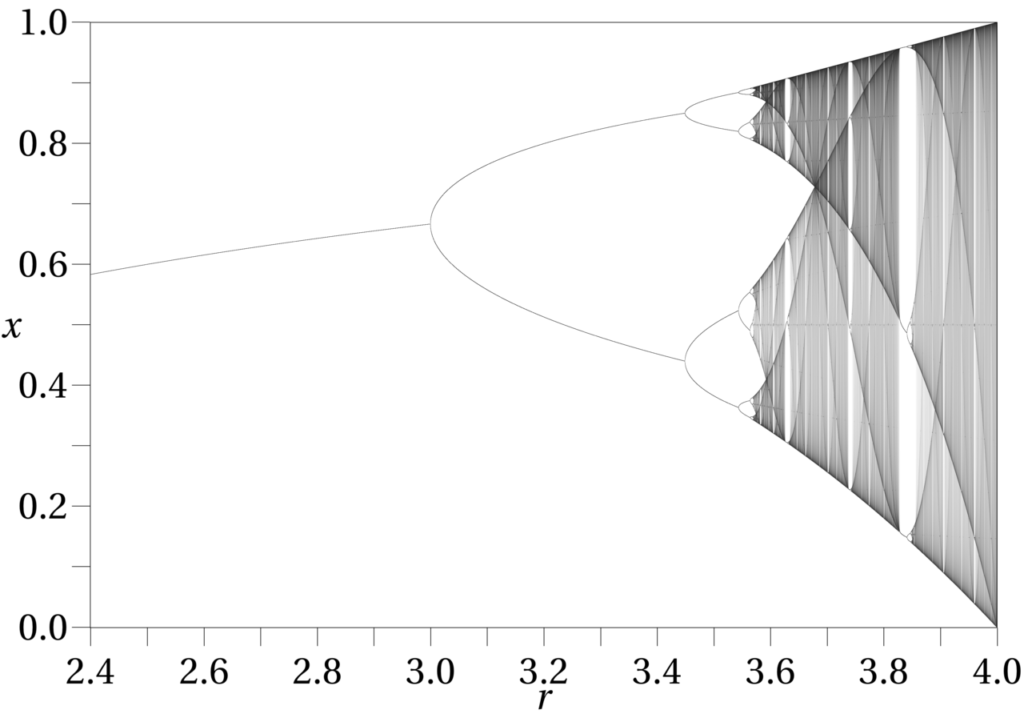
Simple Dynamic Equations Lead to Randomness & Chaos

Robert May took this observation to his mathematician friend James Yorke.

After mathematically analyzing the equation Yorke published an influential paper titled “Period Three implies Chaos”.

It is from this paper that the Chaos Theory derives its name. The key takeaway of the paper was that simple mathematical equations are capable of showing complicated dynamical behavior.

The scientific community initially found the presence of Chaos perplexing. Chaos meant that simple mathematical equations could give birth to complexity and unpredictability, challenging the ‘simple science’ assumptions governing traditional scientific models.

But soon scientists used this characteristic behaviour of the logistic maps to artificially generate pseudo-random numbers. This was the origin of randomness that I was looking for.

Randomness and Chaos is in-built in Complex Dynamic Systems.

Complex Systems are interconnected networks comprising multiple components that dynamically interact and influence each other’s behaviour.

These interactions lead to several properties and behaviours such as spontaneous emergence and disappearance of Randomness and Chaos. These emergent properties and behaviours cannot be understood by analysing the components in isolation.

These findings convey something truly profound about the nature of our world.

The intimate interdependence of Chaos and Order continuously breathes magic into our world. For some this magic is wonderful but for others this magic makes life incredibly difficult.

‘Simple science’ has admirably unraveled the mysteries of order in the world. But comprehending the full intricacies of our universe necessitates embracing the significance and beauty of chaos and randomness.

By grasping the profound link between Order and Chaos, we can gain a far deeper understanding of our world, surpassing the limitations of simple science thinking.

Before we develop this deeper understanding, let’s look at the surprising ways in which the Butterfly effect leads to Chaos and makes our life unfair.